High Pass Filter
Filters are circuits that are used to remove part of a complex AC signal.
A high pass filter is designed to remove unwanted low frequencies from a complex input signal. An ideal high pass filter would pass only frequencies higher than a cut-off frequency.
The process of removing unwanted frequencies is called attenuation. A high pass filter primarily attenuates low frequencies so that the resulting output is comprised of only high frequencies.

High-pass filters don’t create any of the frequencies they output; they simply eliminate high frequencies, leaving only the desired low frequencies.
In the case of active high-pass filters, an amplifier is used to increase the strength of the high frequency signal. The fundamental operation of the filter (attenuating low frequencies) remains the same as a passive high-pass filter.
High-pass filters require capacitive reactance in order to work. They take advantage of the fact that a capacitor’s impedance to an alternating current (AC) source scales with frequency.
High-pass filters are often compared with low pass filters, which also features a resistor and capacitor in the opposite configuration to remove high frequencies from an AC signal.
Comprised of a resistor and capacitor, the cut-off frequency of a filter is determined by the values (i.e. resistance and capacitance) of the two components.
High-pass filters rely on the phenomenon of AC impedance in order to function. Impedance is the opposition to flow of current in AC circuits. In DC circuits, only resistance opposes current but in AC circuits, the flow of electric current is also opposed by capacitors and inductors.
In AC circuits, resistors contribute resistance, just like they do in DC circuits. Capacitors contribute capacitive reactance, which depends on the frequency of the input AC signal. The total impedance is the sum of the resistance and reactance.
Impedance = Resistance + Reactance
Both high and low pass filters take advantage of capacitive reactance, which is frequency dependent. The characteristic cut-off frequency of the filter is due to the value of both the resistance and capacitance.
Ideal High Pass Filter
A high pass filter preferentially attenuates low frequencies, so that high frequencies are allowed to pass while low frequencies are blocked.
An ideal high pass filter would prevent any frequency component above the cut-off frequency from passing, but actual high pass filters aren’t perfect.
Both high and low pass filters use a combination of resistor and capacitor, but the arrangement is reversed in each. A high pass filter has the input signal applied directly to the capacitor, and the output is measured across the resistor.

High Pass Filter Circuit Diagram

A high pass filter consists of a capacitor and resistor in series.
The input waveform Vin is passed through the capacitor, and the output waveform Vout is measured across the resistor.
The fact that the output is measured across the resistor is crucial to the functionality of the filter. It means that the output of the filter is exactly the voltage drop (i.e. potential difference) across the resistor.
Since the total voltage drop across the circuit is Vin, whatever voltage is not dropped across the frequency-dependent capacitor must be dropped across the resistor:
Vout = VR = Vin – VC
Thus the high-pass filter works because the voltage dropped by the capacitor depends on its’ capacitive reactance, which is frequency dependent.
Capacitive Reactance in High-Pass Filters
The overall characteristics of the high pass filter comes from the interplay of capacitive reactance and resistance, which both contribute to the total impedance.
The impedance contributed by the resistor (i.e. resistance) doesn’t depend on the frequency, but the capacitive reactance is inversely proportional to the frequency. This means that at low frequencies, the capacitive reactance is high while at high frequencies, the capacitive reactance is low.
The high-pass filter takes advantage of this by using the capacitor to attenuate low frequencies. The remainder of the input signal passes to the resistor, where the filter output is taken.
The formula for capacitive reactance is as follows:
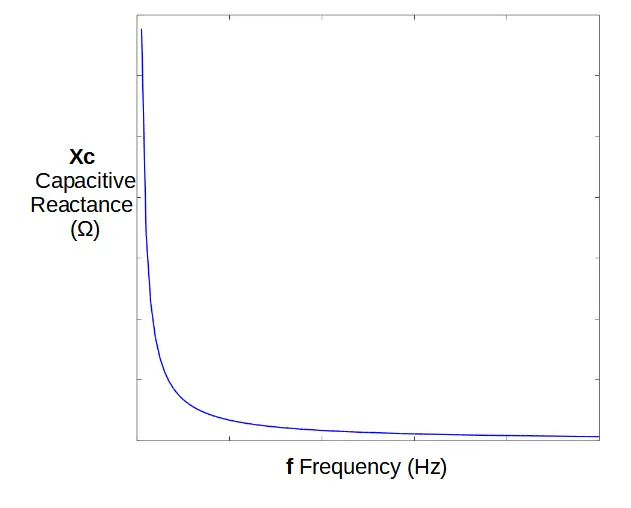
X_C = \frac{1}{\omega C} = \frac{1}{2\pi fC}If we plot capacitive reactance vs. frequency, we can see how the voltage drop across the capacitor changes with frequency.
At low frequencies, the voltage drop is very high. This means that when we measure the output across the resistor, the output voltage of the filter will be very low when the frequency is low. This allows low frequencies to pass through the filter.
At high frequencies, the capacitive reactance is low, so the voltage drop across the capacitor is very low. Most of the voltage is dropped by the resistor. If we measure the voltage output across the resistor, the signal strength will be extremely high. This means that the high frequency output will be high.
Plot of Capacitive Reactance vs. Frequency
Low-Pass Filter Output vs. Frequency
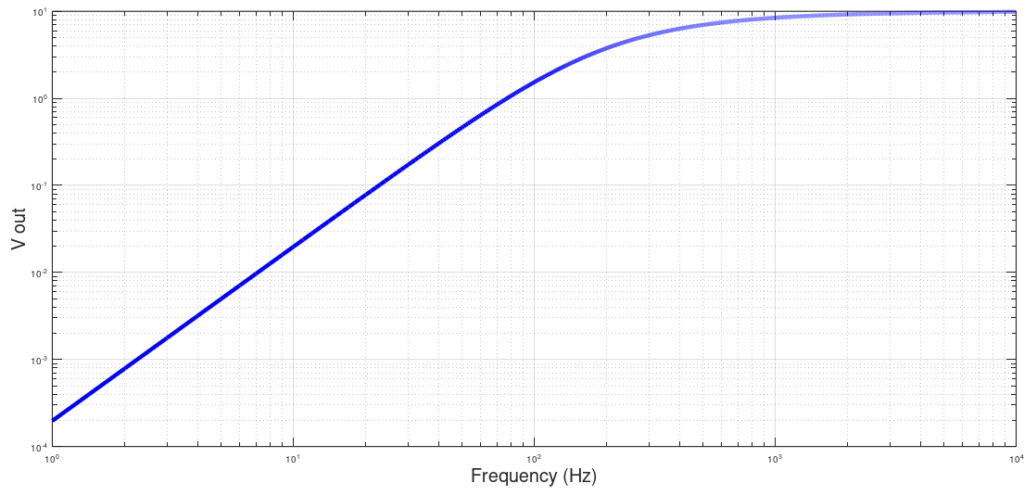
We can confirm this result by plotting the output voltage against frequency.
As we can see, the output voltage is very low at low frequencies and high at high frequencies.
We can also see that real-life high pass filters are not ideal; an ideal high pass filter would have a vertical line at the cut-off frequency. Instead, low frequencies are significantly reduced in power but not removed entirely.
If we were to magnify the curve at high frequencies, we would also see that high frequencies are not allowed to pass perfectly; every frequency experiences some attenuation. The total attenuation is far smaller at high frequencies than it is at low frequencies.
High Pass Filter Cut-Off Frequency
The cut-off frequency fc can be determined by the values of the resistor and capacitor.
f_c = \frac{1}{2 \pi R C}Accordingly, one can determine the value of resistor or capacitor to construct a low pass filter by solving for any value given the others.
To find the value of a resistor given the required cut-off frequency and value of capacitor:
R = \frac{1}{2 \pi f_c C}To find the value of a capacitor given the required cut-off frequency and value of resistor:
C = \frac{1}{2 \pi f_c R}Mathematical Description of High Pass Filter
At low frequencies, the capacitive reactance of the circuit will be high compared with the resistance contributed by the resistor.
We can therefore think about this circuit as a type of tunable voltage divider. Recall the voltage divider formula:
V_{out} = V_{in} \frac{R_2}{R_1 + R_2}=V_{in} \frac{R_2}{R_T}If we substitute capacitive reactance into the formula for the voltage divider, we find the following relation:
V_{out}=V_{in} \frac{R}{Z}Where Z is the total impedance and Xc is the capacitive reactance. The relation between these is given by:
Z = \sqrt{R^2 + X_C^2}If we solve for the output while varying the frequency, we find that low frequencies have a significantly higher output than higher frequencies.
The relation for Vout can be found by substituting the formula for impedance (Z) into the relation between Vin and Vout:
V_{out}=V_{in}\frac{R}{\sqrt{R^2 + X_C^2}}This is shown in the plot of Vout, which we saw earlier.

Summary of High-Pass Filters
We have seen that high-pass filters rely on capacitive reactance in order to generate a high voltage across the capacitor at low frequencies. By configuring the output as the voltage across the resistor, the high-pass filter makes use of the capacitor’s tendency to block low frequencies.
While an ideal high-pass filter would block all frequencies below the cut-off frequency, actual high-pass filters block all frequencies to some degree. This is why amplifiers are often employed after the filter stage. The combination of filter and amplifier is often known as an active high-pass filter.