Capacitors in Parallel

Capacitors are one of the most common circuit components.

Why it’s important: Capacitors store electrical energy, and you can increase the capacitance of a system by placing capacitors in parallel. In this lesson, we will learn that capacitors in parallel add to the capacitance in the system in a similar way to placing resistors in series. You can use this knowledge to engineer a specific value of capacitance from those you already have on hand, or to increase the capacitance beyond that of your highest capacitor.

Review of Capacitance

Capacitors store electric charge when we connect them to a voltage source. This charge comes from the polarization of the insulating material in between the conductive plates of the capacitor.

The capacitance is the ratio of the total charge to the voltage:

C = \frac{Q}{V}

Where Q is the charge (in Coulomb), V is the Voltage, and C is the capacitance.

The SI Unit of capacitance is the Farad, which is defined as 1 Coulomb of charge per 1 Volt of potential difference:

1F = \frac{1C}{1V}

We also saw that capacitance is equal to the permittivity of the dielectric material times the area of the capacitor’s surface, divided by the distance between the conductive plates:

C = \epsilon \frac{A}{d}

Here, ε is the permittivity of the dielectric used, A designated the plate surface area, and d is the distance between the plates.

Two Capacitors in Parallel

When we learned about combining resistors, we saw that two resistors in series effectively function as a single resistor with a total resistance of the sum of both resistors.

With capacitors, we are starting with multiple capacitors in parallel because just as two resistors in series function as one, multiple capacitors in series also function as one. In other words,

C_T = C_1 + C_2 + C_3 +...+C_N

Let’s take a look at the following circuit:

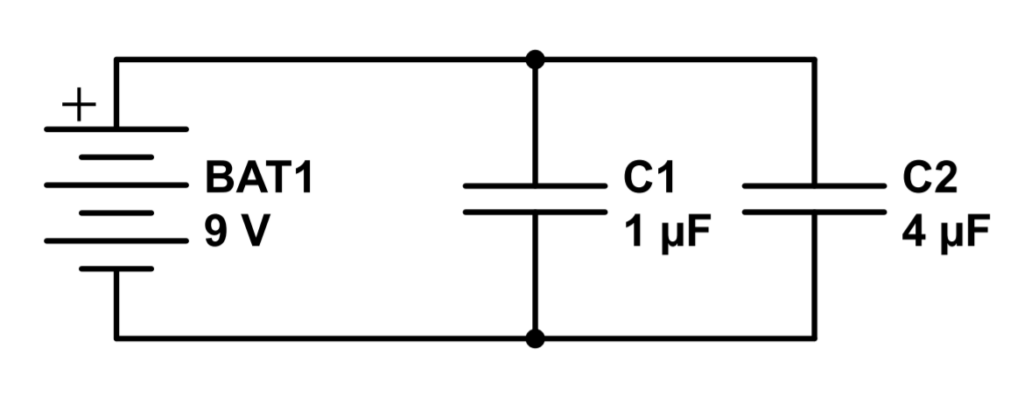
A 1 μF capacitor in parallel with a 4 μF capacitor.

In this circuit, a 1 μF capacitor has been placed in parallel with a 4 μF capacitor.

Example 1:

a) What is the equivalent capacitance of this circuit?

C_T = C_1 + C_2 = 1\mu F + 4\mu F = 5 \mu F

b) How much total charge will be stored in the capacitors of the circuit when fully charged?

Q = CV = (5\mu F)(9V) = 45\mu C

Example 2: Three capacitors in parallel

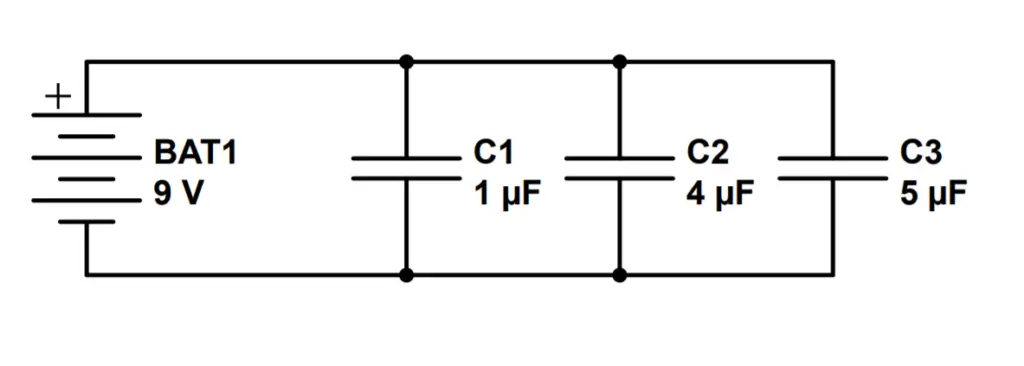
a) What is the equivalent capacitance of this circuit?

C_T = C_1 + C_2 + C_3 = 1\mu F + 4\mu F + 5\mu F = 10 \mu F

b) How much total charge will be stored in the capacitors of this circuit when fully charged?

Q=CV=(10\mu F)(9V)=90\mu C