This DC power calculator is a handy tool for calculating electric power dissipated between two points of a DC circuit using voltage, current, or resistance.
Power in a DC circuit is the measure of the rate of energy dissipated between two points. The unit of measure for electric power is the watt, which is equal to energy/time:
Watts = Energy/time = Joules/second
The power supplied by a DC circuit can be calculated in three (3) different ways. You can use either the voltage and current, voltage and resistance, or resistance and current.
The following calculator will output the power (in watts) dissipated in a current carrying path. Note that the three possible calculations will be identical when Ohm’s Law (V = IR) is followed; otherwise, the three calculations will be different.
Note that this calculator is for DC circuits; for AC circuits, please use the AC power calculator.
Scroll past the calculator for helpful information about how power is calculated using the three methods.
DC Power Calculator
The Three Ways of Calculating Power
The three ways of calculating power are as follows:
Power equals voltage times current:
P = V x I
Power equals the voltage squared divided by resistance:
P = V2/R
Power equals the current squared times resistance:
P = I2R
How Power is Measured
Electric power is measured between two points of a circuit, using the voltage (potential difference) across the two points, the current between the two points, and the resistance of the conductive elements between the two points.
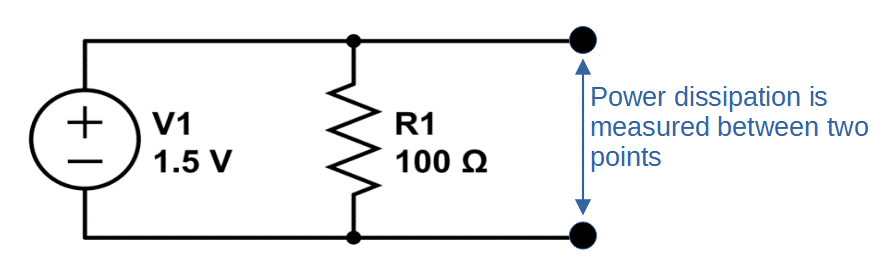
These three quantities are related to each other through Ohm’s Law, V = I x R.
Calculating Power Using Voltage and Current
The most common way to calculate power dissipation is by using the voltage across two points times the current flowing between the points:
Power (P) = Voltage (V) x Current (I)
P = V x I
Calculating Power Using Voltage and Resistance
Using Ohm’s Law, we can substitute the current from the above equation to find power as a function of voltage and resistance:
P = V x I
I = V/R
P = V x (V/R) = V2/R
Calculating Power Using Current and Resistance
Again using Ohm’s Law, we can substitute the value for voltage to find power as a function of current and resistance:
P = V x I
V = I x R
P = (I x R) x I = I2R
Understanding Power By Using Unit Analysis
It is helpful to compare units in order to better understand what power actually represents.
Voltage is measured in volts, which is joules per coulomb, or energy per unit of electric charge. You can think of volts as the energy per unit of charge that is dissipated as the charge flows between the two measurement points, from the point of high potential to the point of low potential.
Volts = Joules/Coulomb
Current is measured in amps, which is coulombs per second. You can think of current as the rate of electric charge flowing between the two measurement points:
Amps = Coulombs/second
Since power is the voltage times the current, the unit of coulombs from each cancels out, and we are left with the energy dissipated over time:
Power = Voltage x Current = Joules/Coulomb x Coulomb/second = Joules/second