Circuits that have both resistive and capacitive elements (called RC circuits) take time to charge and discharge. During that time, the voltage across the capacitor is constantly changing.
The calculator on this page will automatically determine the time constant, electric charge, time to fully charge or discharge, and the total voltage while charging or discharging.
An explanation of each calculation can be found below the calculator.

RC Time Constant Calculator
The first result that can be determined using the calculator above is the RC time constant. It requires the input of the value of the resistor and the value of the capacitor.
The time constant, abbreviated T or τ (tau) is the most common way of characterizing an RC circuit’s charge and discharge curves.
T is equal to the value of the resistor (in ohms) times the value of the capacitor (in farads):
T = \tau = RC
The time constant comes from the equations for the charge and discharge of the capacitor:
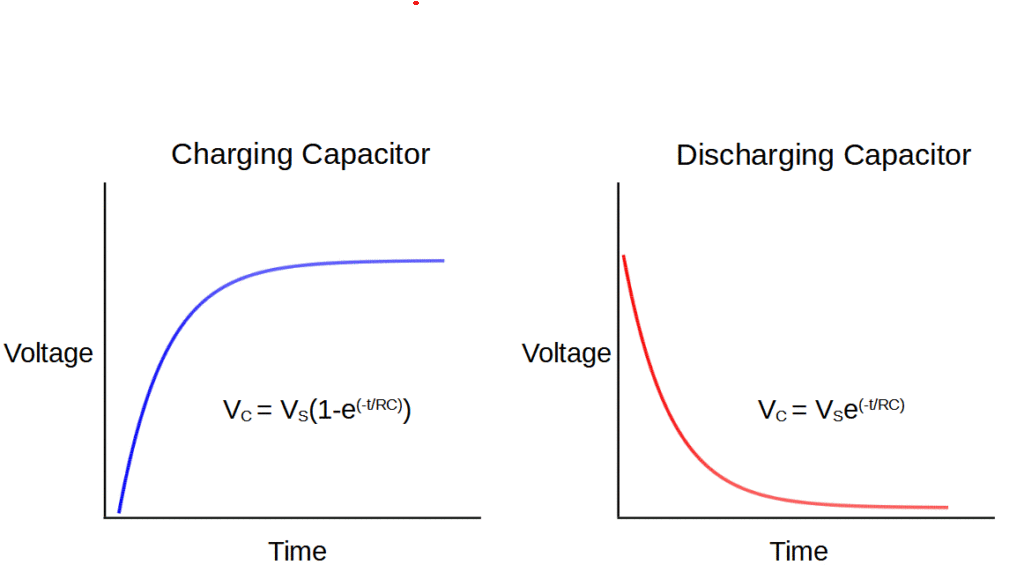
Voltage at time ‘t’ while charging:
V_C(charging) = V_s (1-e^{-\frac{t}{RC}})=V_s(1- e^{-\frac{t}{\tau}})VC is the voltage across the capacitor, and VS is the source voltage.
Voltage at time ‘t’ while discharging:
V_C(discharging) = V_s e^{-\frac{t}{RC}}=V_s e^{-\frac{t}{\tau}}The time constant, RC, is the time it takes for the voltage across the capacitor to charge or discharge 63.2%, which is equal to e-1.
Capacitor Electric Charge Calculator
The amount of electric charge that has accumulated on the plates of the capacitor can be calculated if the voltage and capacitance are known.
The total charge (Q) is equal to the capacitance (C) times the source voltage (V):
Q=CV
Capacitor Charge and Discharge Calculator
The calculator above can be used to calculate the time required to fully charge or discharge the capacitor in an RC circuit.
The time it takes to ‘fully’ (99%) charge or discharge is equal to 5 times the RC time constant:
Time \, to \, 99 \% \, discharge =5RC=5\tau=5T
Like the time constant itself, it requires the value of the resistor and capacitor in the RC circuit. If you require the capacitor to discharge in a certain period of time, you can also use this formula to determine the value of resistor or capacitor needed.
Capacitor Voltage While Charging Calculator
The voltage across the capacitor at any time ‘t’ while charging can be determined using the calculator above. To do so, it requires the values of the resistor and capacitor, as well as the time ‘t’ at which we want to find the voltage.
A charging capacitor obeys the following equation:
V_C(charging) = V_s (1-e^{-\frac{t}{RC}})=V_s(1- e^{-\frac{t}{\tau}})Where VS is the source voltage and e is the mathematical constant (Euler’s number), e~ 2.71828.
Capacitor Voltage While Discharging Calculator
The voltage across the capacitor at any time ‘t’ while discharging can be determined using the calculator above. To do so, it requires the values of the resistor and capacitor, as well as the time ‘t’ at which we want to find the voltage.
A discharging capacitor obeys the following equation:
V_C(discharging) = V_s e^{-\frac{t}{RC}}=V_s e^{-\frac{t}{\tau}}Where VS is the source voltage and e is the mathematical constant (Euler’s number), e~ 2.71828.
If these calculators didn’t help, check out our other calculators for electronics or our comprehensive tutorials!