Electric Power

Electric power is the rate at which electrical energy is transferred by an electric circuit.

Electric power determines the work that can be done by a circuit, in a given amount of time. Note that work has the same units as energy; it is essentially energy that is used to do something productive.

In a circuit, electric power is also equal to the voltage times the current:

Power (P) = Voltage (V) x Current (I)

Here, the term voltage refers to the ‘voltage drop‘, which is the drop in electric potential as current flows through a circuit, doing useful things like powering lightbulbs, heaters, or refrigerators.

When you receive an electric bill from an electric power company you are billed for using energy. The relationship between energy and power can seem daunting, but it’s actually quite simple. Electric power is equal to energy per second; energy per unit time. The total energy that you are billed for is therefore a unit of power – typically a kilowatt – multiplied by a unit of time – typically an hour. That’s where the unit ‘kilowatt-hour’ (kWh) comes from.

What is Electric Power?

The most general definition of power (not only electrical power) is the amount of energy transferred per unit time. In other words, power is the rate of energy transfer.

So the most general definition of electric power is therefore: electric power is the rate at which electrical energy is transferred by an electric circuit.

Let’s look at this definition and try to understand it one piece at a time:

Electric power is a rate. In other word, something is happening over time. Therefore, we should expect power to be equal to ‘something’ over (i.e. divided by) a unit of time, which is typically seconds.

Electric power is the rate at which electrical energy is transferred. Just like mechanical power, electric power is a rate of energy transfer. In the case of electrical power, we are normally concerned with how electrical energy is used in circuits.

The Three Ways of Calculating Power

The three ways of calculating power are as follows:

Power equals voltage times current:

P = V x I

Power equals the voltage squared divided by resistance:

P = V²/R

Power equals the current squared times resistance:

P = I²R

How Power is Measured

Electric power is measured between two points of a circuit, using the voltage (potential difference) across the two points, the current between the two points, and the resistance of the conductive elements between the two points.

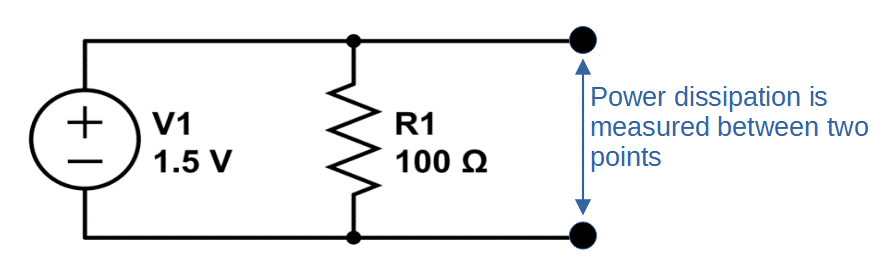
These three quantities are related to each other through Ohm’s Law, V = I x R.

Electric Power Generation and Use

Electric power is often defined as a quantity that is used in circuits, but it must first be generated in order to be consumed. Generation is the act of converting a non-electrical energy into electrical energy. For example, a generator converts the mechanical energy of a spinning shaft into electricity, and a battery converts the energy from a chemical reaction into electricity.

The process of electric power generation and use go hand in hand with each other. When power is used in a circuit, it is simultaneously generated in order to facilitate its’ usage. The amount of power supplied is equal to the amount of power being used.

Active and Passive Circuit Components

It may be helpful to think about electric circuits as a collection of components.

Some circuit components contribute power, and are called power sources, or active devices. Common examples of active devices are batteries, generators, power supplies, and AC adapters.

Other circuit components do not generate power; they either consume power, or store and release it. These components are called passive devices. Common examples of passive devices are resistors, capacitors, inductors, transformers, and diodes.

The Watt – SI Unit of Electric Power

The SI Unit for power is the watt, which is defined as 1 joule per second. Joule is the SI unit for energy, so it makes sense that the watt, which is energy per unit time, is given in joules per second.

The abbreviation for the watt is the letter ‘W’. Keep in mind however that the power is typically denoted in mathematical relations with the letter ‘P’.

Note that the watt is the standard unit for power, be it mechanical, electrical, or any other form of power.

Power = Energy / Time

1\, Watt = \frac{1\, Joule}{1\, Second} => W = \frac{J}{s}

Unit Analysis

Units are a useful way of gaining insight into the nature of the quantity being measured.

Joules are the SI unit for energy, and the SI unit for time is the second. Thus we can see that power, which is measured in watts, is a unit of energy over time; i.e. a rate of energy transfer.

Another interesting aspect of power is that this formula applies not only to electrical power, but any form of energy transfer like mechanical or chemical energy. This is why power is used to relate the electricity generated by AC generators or produced by the chemical reactions in a battery. In contrast, units like voltage, current, and resistance are directly (and only) tied to electrical phenomena.

Derivation of Electric Power

Electric power is the rate of work done by the electric field that is generated when a voltage is supplied to a circuit.

When we supply a voltage to a circuit by connecting a voltage source (like a battery), an electric field is generated, which is defined as the force exerted per unit charge:

(1) \; \;Electric\, Field \, (E)= \frac{Force\, (F)}{Charge\, (q)} => E =\frac{F}{q}

Where E is the strength of the electric field, F is the force, and q is the charge.

For a constant electric field, voltage is the electric field times the distance between the points being measured:

(2) \;\;Voltage\, (V) = Electric\, Field\, (E) \times Distance\, (d) => V =E \times d

If we substitute the equation for the electric field (1) into the equation for voltage (2), we find the following relation:

V= E \times d = (\frac{F}{q}) \times d = \frac{F \times d}{q}

But work is equal to the force times the distance:

Work\, (W)= Force\, (F) \times distance\, (d) => W =F \times d

So the voltage is equal to the work divided by the charge:

V = \frac{F\, \times d}{q} = \frac{W}{q}

Power is defined as the rate of work being done. If we rearrange the above equation:

Power\, (P) = \frac{Work\, (W)}{time\, (t)} => P =\frac{W}{t}=\frac{V\times q}{t} = V\times \frac{q}{t}

We also know that current is defined as charge per unit time:

Current\, (I) = \frac{charge (q)}{time\, (t)} => I=\frac{q}{t}

If we substitute this equation of current into the equation, we find the most popular definition of electric power in a circuit: power equals voltage times current:

Power\, (P) = Voltage \, (V) \times Current \, (I) =>P = VI

One thing to keep in mind is that voltage here refers to a voltage drop, i.e. potential difference across a resistive component or section of circuit. The power supplied is equal to the power dissipated by the electrically resistive elements in the circuit.

Power Dissipation and Joule Heating

Power dissipation is the loss of power due to electrical resistance. In any circuit with resistive properties (technically any circuit), there will be power dissipation. Even conductors have some resistance.

As electrons travel through the material, they collide with atoms, grain boundaries, and other defects (see the lesson on electrical resistance for more information). Each time an electron is deflected from its path of travel, it loses a little bit of energy; that energy is lost as heat from the collision (also known as a scattering event).

Given our formula: P = V x I, we can use Ohm’s Law to see that the following relation is also true:

Ohm's \, Law: V=I \times R \\
... \\
P = I \times V = I \times (I \times R) = I^2R

So the power dissipation is equal to I²R. This term is widely known as an ‘I-squared-R loss’ and is also known as Joule heating. Given a resistance value and the current, we can determine the power dissipation using the above formula.

If we happen to know the voltage but not the current, we can also use Ohm’s Law to solve for the power dissipation in an alternate way:

P  = I \times V = (V \times R) \times V = \frac{V^2}{R}

Using Power to Calculate Required Resistance

In many cases, electrical components are rated with a maximum power tolerance. Above this maximum power level, the component may fail, arc, or even explode.

One of the most useful calculations when first creating a circuit is to determine the required resistance in order to protect the circuit components and prevent accidental damage or bodily harm!

We can use the above formulas to calculate the resistance that we need to use in order to protect a circuit component.

If we know the voltage across the resistor, we can use the following formula:

P = \frac{V^2}{R}

Rearranging this, we find:

R = \frac{V^2}{P}

Given a voltage source, we can square the value of the voltage and divide by the power rating of the component in order to determine the needed size of resistor.

Keep in mind that this should be performed for the component with the lowest power rating in the circuit. It could be the resistor itself!

Congratulations!

You have successfully completed Module 2, and now have a good understanding of some of the most important topics in the fields of electronics and physics.

Module 3 will build on all of these concepts. We’ll work through lots of problems and strengthen our ability to read electrical schematics. By the time you’re done, the topics from Module 2 will be second nature to you.

Let’s continue on to Module 3!