This page contains a variety of calculators as an aid in learning about and designing with capacitors.
It contains calculators for the equivalent capacitance of capacitors in series and parallel, a calculator for the reactance of a capacitor in an AC circuit, and a charge, discharge, times constant, and voltage calculator.
Capacitors in Series Calculator
Main Page: Capacitors in Series Calculator
The capacitors in series calculator (just below) takes the values of up to four (4) capacitors and calculates the equivalent capacitance.
In a series circuit, current must flow through every circuit component; there is only one current path. Capacitance, in particular, decreases with every additional capacitor in a series circuit. In the series circuit on the right, each individual capacitor (C1, C2 and C3) would contribute more capacitance to the circuit than the three combined.
To use the calculator, first select the number of capacitors. Enter the capacitor values sequentially, starting with C1.
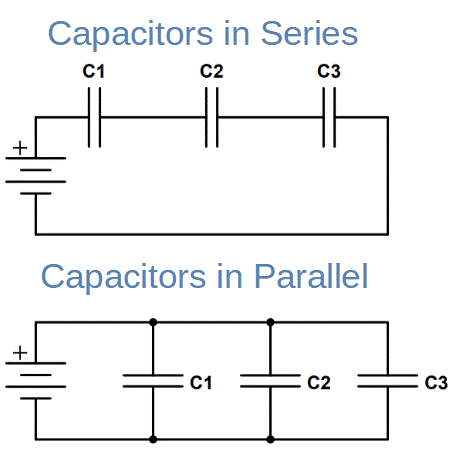
To find the total capacitance in a series circuit (or a single branch of a parallel circuit), you find the reciprocal (‘ one over 1/ ‘) of the sum of the reciprocal of each individual value of capacitance:
C_{eq} = \frac{1}{\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+...+\frac{1}{C_N}}=(\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+...+\frac{1}{C_N})^{-1}Capacitors in Parallel Calculator
Main Page: Capacitors in Parallel Calculator
The capacitors in parallel calculator takes the values of up to four (4) capacitors and calculates the equivalent capacitance.
In a parallel circuit, current has more than one path to flow through. If each path contains a capacitor, the effect is additive. The capacitors each contribute so that the total capacitance is greater than any of the capacitors individually.
To use the calculator, first select the number of capacitors. Enter the capacitor values sequentially, starting with C1.
To find the total capacitance in a parallel circuit (or a single branch of a parallel circuit), you just add up the capacitances of everything in the circuit (or branch):
C_{eq} = C_1 +C_2+C_3+...+C_N
Capacitor Reactance Calculator
Main Page: Capacitor Reactance Calculator
The capacitive reactance calculator (just below) can be used to determine the opposition to current flow (in ohms) by a capacitor in an AC circuit.
To use the calculator, input the frequency of the AC signal and the value of the capacitor. It will output the reactance in ohms.
Capacitive reactance (abbreviated XC) is a frequency dependent term. It determines the voltage drop across the capacitor in an AC circuit. Like resistance, which determines the voltage across a resistor, capacitive reactance is measured in ohms.
The following equation expresses capacitive reactance as a function of both frequency (f) and capacitance (C):
X_C = \frac{1}{\omega C} = \frac{1}{2\pi fC}Capacitor Charge, Discharge, Time Constant and Voltage Calculator
Main Page: Capacitor Charge and Discharge Calculator
Circuits that have both resistive and capacitive elements (called RC circuits) take time to charge and discharge. During that time, the voltage across the capacitor is constantly changing.
The time constant, abbreviated T or τ (tau) is the most common way of characterizing an RC circuit’s charge and discharge curves.
Use the calculator below to determine the time, constant, electric charge, time to fully charge or discharge, and the voltage at any given time while charging or discharging.
The time constant (T or τ) is equal to the value of the resistor (in ohms) times the value of the capacitor (in farads):
T = \tau = RC
The time constant comes from the equations for the charge and discharge of the capacitor:
Voltage at time ‘t’ while charging:
V_C(charging) = V_s (1-e^{-\frac{t}{RC}})=V_s(1- e^{-\frac{t}{\tau}})VC is the voltage across the capacitor, and VS is the source voltage.
Voltage at time ‘t’ while discharging:
V_C(discharging) = V_s e^{-\frac{t}{RC}}=V_s e^{-\frac{t}{\tau}}The time constant, RC, is the time it takes for the voltage across the capacitor to charge or discharge 63.2%, which is equal to e-1.
If these calculators didn’t help, check out our other calculators for electronics or our comprehensive tutorials!