Wheatstone Bridge

A Wheatstone bridge is a circuit that uses three resistors and a voltmeter to measure an unknown quantity of electrical resistance.

The Wheatstone bridge is constructed by connecting two sets of two resistances in series/parallel bridge configuration. A voltmeter connects the two branches.

In the circuit above, R_x (the resistor on the lower right) is the unknown resistance that will be measured. R₁ and R₃ are resistors with known resistance values, and R₂ is a potentiometer (an adjustable resistor). The circle in the middle labeled V_G is a voltmeter; originally this would have been a galvanometer, hence the ‘G’ subscript.

While we would probably just use a multimeter to measure resistance today, the Wheatstone bridge continues to be used as a common example for further understand basic principles of analog resistive circuits.

Alternate Wheatstone Bridge Circuit Diagram

Although the Wheatstone bridge circuit is traditionally shown using the diamond configuration (which we use throughout this article), it is electrically identical to the series-parallel resistor circuit shown below:

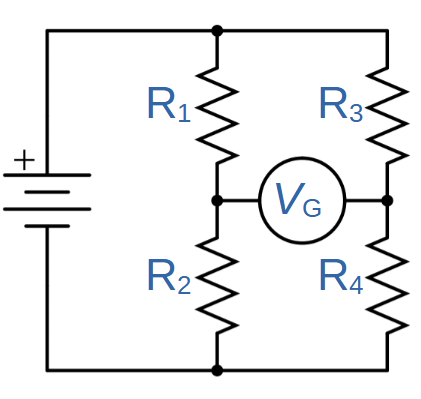
It’s a useful exercise to prove this to yourself and to understand why we can use different layouts to show the same circuit.

Balanced Wheatstone Bridge

A Wheatstone bridge circuit is known as either balanced or unbalanced depending on the values of the resistors.

The first scenario is a properly balanced Wheatstone bridge circuit.

Balanced means that no current flows through the voltmeter in the middle; in other words, V_G = 0.

This is shown in the figure below (note 0 V through the voltmeter):

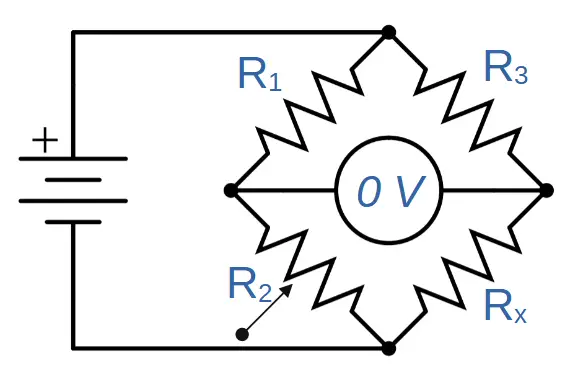
In order for the circuit to be balanced, the points being measured must be at the same voltage. In other words, the voltage drop across R₁ and R₃ must be equal.

This condition is established by the ratios of resistance values. If the ratio between the resistors on the left (R₁ and R₂) and resistors on the right (R₃, and R_x) are equal, then the circuit will be balanced and current won’t flow through the voltmeter:

\frac{R_1}{R_2}=\frac{R_3}{R_x}

We can solve for R_x:

R_x=\frac{R_2R_3}{R_1}

So if R₁, R₂, R₃, and are all known, we can find the value of R_x.

How a Wheatstone Bridge Circuit Works

The Wheatstone bridge circuit uses the potentiometer (R₂) and voltmeter (V_G) together.

When the circuit is first constructed, chances are high that the circuit will be unbalanced. The voltmeter will measure a voltage difference between the right and left sides of the circuit (V_G ≠ 0).

The potentiometer is then adjusted until the voltmeter measures zero volts, i.e. V_G = 0.

Once the voltage measures zero and the circuit is balanced, the unknown resistance can be determined using the equation for R_x:

R_x=\frac{R_2R_3}{R_1}

Different Wheatstone Bridge Configurations

The equations given above allow us to solve for an unknown resistance in all four of the possible locations.

If we change the value of R_x to R₄, we can use the following diagram to solve for each of the different resistor locations in the Wheatstone bridge.

R_1=\frac{R_2R_3}{R_4}

R_2=\frac{R_1R_4}{R_3}

R_3=\frac{R_1R_4}{R_2}

Wheatstone Bridge Problem No. 1

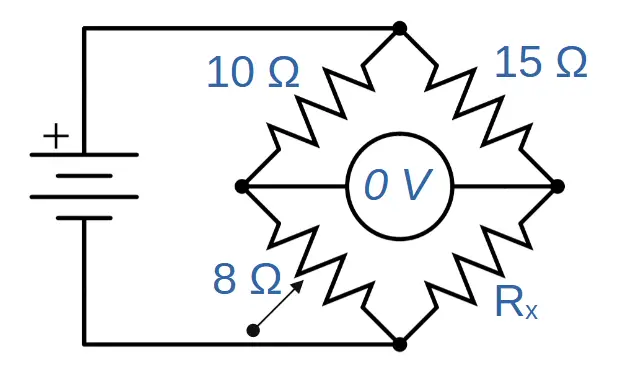
You have three resistors with known values connected in a circuit as shown.

Resistor R₁ is 10 ohms, resistor R₂ is 8 ohms, resistor R₃ is 15 ohms and the unknown resistance is R_x. The voltmeter shows measures 0 volts indicating a balanced circuit.

What is the value of resistor R_x?

Using the Wheatstone bridge formula above:

R_x=\frac{R_2R_3}{R_1}=\frac{(8\Omega)(15\Omega)}{(10\Omega)}=\frac{120\Omega ^2}{10\Omega}=12 \Omega

Using the classic Wheatstone bridge problem, we find that the value of R_x must be twelve ohms (12Ω).

Wheatstone Bridge Problem No. 2

What value of resistor R₂ will balance the circuit shown below?

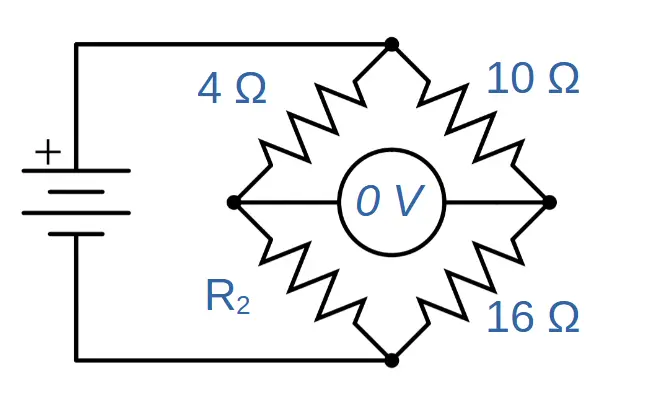
This time R₂ is the unknown resistance. How can we find it?

Resistor R₁ is 4 ohms, resistor R₃ is 10 ohms and resistor R₄ is 16 ohms. The voltmeter measures 0 volts, indicating a balanced circuit.

We can always use the ratios of the resistance values between the left and right sides to find any unknown resistance in a balanced circuit.

Since we’re solving for R₂, let’s put that on top. Then, the ratio of R₂ to R₁ will be equal to the ratio of R₄ to R₃:

\frac{R_2}{R_1}=\frac{R_4}{R_3}

We can solve for R₂ by multiplying both sides by R₁:

R_2=\frac{R_1R_4}{R_3}=\frac{(4\Omega)(16\Omega)}{10\Omega}=\frac{64\Omega^2}{10\Omega}=6.4\Omega

Kirchhoff’s Laws for Wheatstone Bridge

A deeper analysis of the Wheatstone bridge can be performed by using Kirchoff’s current and voltage laws.

Kirchhoff’s Current Law for Wheatstone Bridge

Kirchhoff’s current law (KCL) states that the electric current flowing into a junction must equal the current flowing out of that junction.

Let’s see how this applies to the Wheatstone bridge.

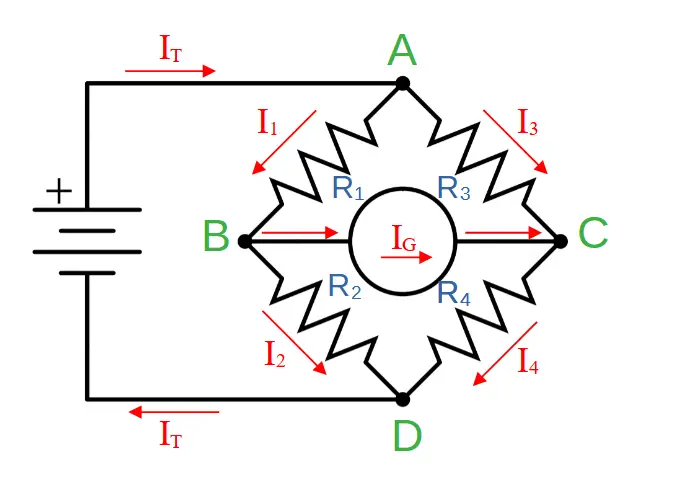
In the circuit above, we have labeled the four junctions of the circuit A, B, C, and D.

We have also labeled the current through R₁ as I₁, the current through R₂ as I₂, the current through R₃ as I₃, and the current through R₄ as I₄.

The total current flowing into and out of the battery is labeled I_T, and the current through the voltmeter/galvanometer is labeled I_G.

Since we have four junctions, we can set up four equations using KCL:

KCL for Junction A:

Current flowing into junction A = Current flowing out of junction A

(1) I_T = I₁ + I₃

KCL for Junction B:

Current flowing into junction B = Current flowing out of junction B

(2) I₁ = I₂ + I_G

KCL for Junction C:

Current flowing into junction C = Current flowing out of junction C

(3) I₃ + I_G = I₄

KCL for Junction D:

Current flowing into junction D = Current flowing out of junction D

(4) I₂ + I₄ = I_T

KCL with Balanced Wheatstone Bridge

When the Wheatstone bridge circuit is balanced, I_G will equal zero (I_G = 0).

In that case, we can rewrite equations (2) and (3):

(2b) I₁ = I₂ + I_G => I₁ = I₂

(3b) I₃ + I_G = I₄ => I₃ = I₄

We’ll use these results combined with Kirchhoff’s Voltage Law to derive the relationship between resistors in a balanced circuit.

Kirchhoff’s Voltage Law for Wheatstone Bridge

Kirchhoff’s voltage law (KVL) states that for any loop in the circuit, the total voltage must equal zero.

We can divide the circuit into two loops: ABC (or ABCA) and BCD (or BCDB). Let’s use KVL to form an equation for each loop.

Remember that the sign for each term is determined by the direction that we have assumed current will travel in (see the lesson on KVL for more information).

KVL for Loop # 1 (ABCA)

Voltage across R₁ (V₁) + Voltage across galvanometer (V_G) – Voltage across R₃ (V₃) = 0

(5) V₁ + V_G – V₃ = 0

Using Ohm’s Law (V = IR), we can restate this in terms of current and resistance:

(6) I₁R₁ + I_GR_G – I₃R₃ = 0

KVL for Loop # 2 (BCDB)

Voltage across galvanometer (V_G) + Voltage across R₄ (V₄) – Voltage across R₂ (V₂) = 0

(7) V_G + V₄ – V₂ = 0

(8) I_GR_G + I₄R₄ – I₂R₂ = 0

KVL With Balanced Wheatstone Bridge

Under balanced conditions, IG = 0 so that equations (6) and (8) can be rewritten:

(6b) I₁R₁ = I₃R₃

(8b) I₄R₄ = I₂R₂

If we multiply equation (8b) by equation (6b), we can solve for R₄:

I_4R_4(I_1R_1)=I_2R_2(I_3R_3)

R_4=\frac{I_2R_2I_3R_3}{I_1R_1I_4}

Now we can simplify using the results we found from KCL in a balanced circuit (I₁ = I₂) and (I₃ = I₄). We can use these relations to cancel out the two current terms in the numerator with the two in the denominator:

R_4=(\frac{I_2I_3}{I_1I_4})\frac{R_2R_3}{R_1}=(1)\frac{R_2R_3}{R_1}

R_4=\frac{R_2R_3}{R_1}

We have successfully used KCL and KVL to derive the relation between the resistances in a balanced Wheatstone bridge circuit.

Bridge Circuits

The Wheatstone bridge is the most popular example of a bridge circuit.

A bridge circuit is characterized by having two branches of electric circuit that are connected by a third branch that bridges them.

Variations of the Wheatstone bridge include the Wien bridge, Maxwell bridge, and Heaviside bridge.

A variation on the bridge circuit is also used in the bridge rectifier, where four diodes are used to change DC current into AC.

Like many bridge circuits, the Wheatstone bridge is a clever way of using basic electrical principles to achieve an interesting goal.