The reactance of a capacitor is the impedance that it contributes to an AC circuit.
In DC circuits, the capacitor will allow current to flow only while it is charging or discharging. Once the capacitor is fully charged or discharged, it functions as an open circuit.
But in AC circuits, current is allowed to flow at all times because it is constantly changing, so the capacitor is always either charging or discharging.
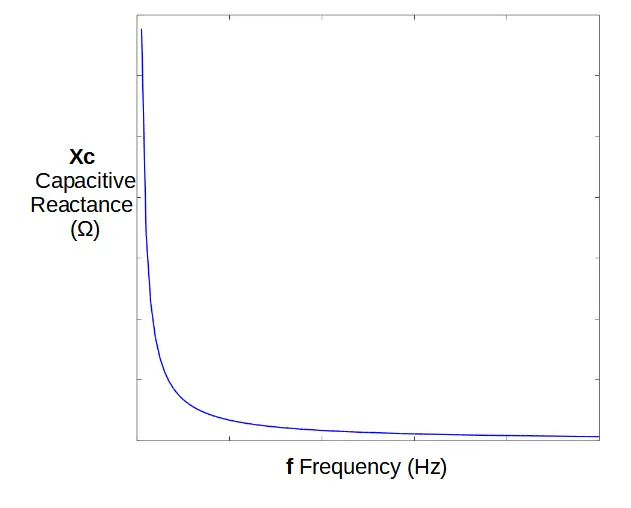
Capacitive reactance is the opposition to AC current flow. It is measured on Ohms (like resistance) and is inversely proportional to the frequency and the value of the capacitor:
X_C = \frac{1}{\omega C} = \frac{1}{2\pi fC}Capacitive Reactance Calculator
Review of Capacitive Reactance
Capacitive reactance (abbreviated XC) is a frequency dependent term, and determines the voltage drop across the capacitor in an AC circuit. Like resistance, which determines the voltage across a resistor, capacitive reactance is measured in ohms.
| Type of Impedance | Determines the voltage across | Unit | Formula |
| Resistance | Resistor | Ohms | R = V/I |
| Capacitive Reactance | Capacitor | Ohms | XC = 1/(2πfC) |
| Inductive Reactance | Inductor | Ohms | XL = 2πfL |
The following equation expresses capacitive reactance as a function of both frequency (f) and capacitance (C):
X_C = \frac{1}{\omega C} = \frac{1}{2\pi fC}Omega (ω) is the angular frequency, and is used to simplify the formula. The angular frequency (ω) is equal to 2 times π times the frequency of the AC signal. It’s also equal to 2π over the period, T:
\omega=2\pi f=\frac{2\pi}{T}The greater the frequency (or capacitance), the lower the capacitive reactance. This is why capacitors are said to function as an open circuit for direct current (DC) but a short circuit at high alternating current (AC) frequencies.
The fact that capacitive reactance depends on the frequency makes it useful in many different filter circuits.