Ohm’s Law
Ohm’s Law is considered one of the most important formulas in the fields of physics and electricity. Ohm’s Law describes the relationship between voltage, current, and resistance.
Ohm’s Law states that the current through two points of a conductor is linearly proportional to the voltage, and defines electrical resistance as the ratio between the voltage and current. It is expressed by the formula:
V = IR
Which means ‘voltage (V) is equal to the current (I) times the resistance (R)’.
By exploring Ohm’s Law, we gain valuable insight into the relationship between three important concepts that are critical to every electrical circuit and electronic device.
Pro Tip: Check out our Ohm’s Law Calculator for a handy reference!

Ohm’s Law: Voltage, Current, and Resistance
Up to this point, we have explored the concepts of voltage, current, and resistance.
| Property | Symbol | SI Unit | Ohm’s Law |
| Voltage | V (or E) | Volt (V) | V = I x R |
| Current | I | Amp (A) | I = V / R |
| Resistance | R | Ohm (Ω) | R = V / I |
Voltage
Voltage is the electrical potential difference between two points in any circuit. Voltage is the energetic ‘push’ that causes electrons to move, creating electrical current. Voltage is measured in units of volts, which is a ratio of energy to charge: 1 volt equals one joule of energy per coulomb of charge.
There are technically two quantities that are measured in volts:
(1) Electromotive force (EMF) is the energy per unit of electric charge (electric potential) supplied to a circuit by a power source like a generator or battery.
(2) Voltage, which describes the equivalent loss in electric potential (called a voltage ‘drop‘) as electric charge travels through a circuit.
A good way to think about voltage is ‘energy per unit of electric charge’, or ‘how much energy is given to and dissipated by each electron’.
Ohm’s law tells us that the voltage ‘drop’ across any part of a circuit is equal to the current through the circuit times the resistance between those two points.
Current
Current is the flow of electric charge (i.e. electrons) through any given point in a circuit.
When we apply a suitable voltage to a closed circuit, electrons will flow through the circuit. Current is the measure of that flow. The unit of measurement for current is amperes, or coulombs (electrical charge) per second.
Ohm’s Law tells us that the current through a path in a circuit is equal to the voltage divided by the resistance.
Resistance
Resistance is the opposition to current flow from one point to another in a circuit.
Resistance is intentionally contributed by resistors, but everything in a circuit adds some resistance. This includes conducting wires, interconnections, and components other than resistors.
Most materials do not have free electrons, so they have high electrical resistance. Some materials have free electrons available for conduction, and the internal structure determines how good they are at conducting electricity. The better a material is at conducting, the lower its resistance. Resistance is measured in the unit Ohm, which is defined as 1 volt (potential difference or ‘drop’) per 1 ampere applied to the material. This relation actually describes Ohm’s Law in terms of units.
Ohm’s law tells us that resistance is the ratio of voltage to current. A very low resistance value will therefore result in a very high current, and a high resistance value will result in a low current (if the applied voltage is kept constant).
Ohm’s Law: The Relationship Between Voltage, Current, and Resistance
The significance of Ohm’s Law is that it describes the relationship between voltage, current, and resistance.
Although Ohm’s Law seems almost obvious today, it actually took many years of scientific experimentation and theory before George Ohm published his famous Law. It wasn’t easily accepted, either; scientists around the world denounced Ohm and his law. It took almost 30 years before his work was widely accepted by the scientific community.
Ohm’s Law Triangle
Ohm’s Law is commonly represented in a triangular format. This format can be helpful in remembering or determining the formulations of Ohm’s Law.
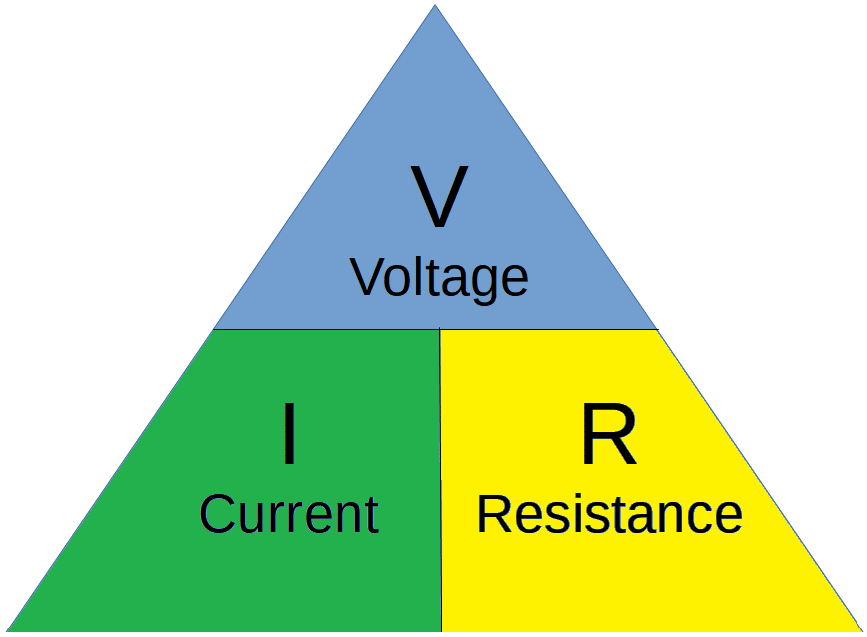
There are three possible terms to solve for: voltage, current, and resistance.
The triangle allows us to solve for any of the three terms without having to memorize the equation (or in case we forget).
To use the triangle to solve for each one, you simply ignore the term being solved for.
For example, to solve for voltage (V) you ignore the top of the triangle (voltage) and are left with IR. Therefore, V = IR.

To solve for current, you ignore the lower left and are left with V over R; voltage over resistance.
To solve for resistance, you ignore the resistance block on the lower right and are left with V over I; voltage over current.
What is Ohm’s Law?
Ohm’s Law states that the voltage (V) is equal to the current (I) times the resistance (R):
V = IR
Written as ‘V = IR’, Ohm’s Law tells us that the voltage, or potential difference (also called voltage ‘drop’) is equal to the current times the resistance of the circuit between the two points. If the current is increased, the voltage drop will also increase. If the resistance of the circuit between the points being measured is increased, the voltage drop will also increase.
You can re-write this to calculate the current:
I = \frac{V}{R}This tells us that the current increases when the voltage is increased, and decreases as the resistance is increased.
If the voltage across that section is increased (by adding a battery, for instance), the current (charge flow) in the circuit will also increase. If the resistance across the section is increased (by adding a resistor), the current will decrease. Voltage is proportional to the current but resistance is inversely proportional. Decrease the resistance, and current will increase.
If the resistance is extremely low, for example, in a circuit without a resistor, the current will be extremely high, which explains why it’s so important to always have a resistor (or resistive element like a lightbulb) in every current carrying path of a circuit.
We can also solve for resistance as the ratio of voltage to current:
R = \frac{V}{I}Thinking about resistance as the ratio of voltage to current can help us better understand the nature of these principles. A 1 ohm resistor will yield 1 amp of current for every 1 volt (1 joule per coulomb of charge) supplied to the circuit by a battery.
If you increase the voltage, you increase the resistance. If you increase the current, you decrease the resistance. One important thing to note however is that resistance is defined by the material, not the applied voltage or resulting current. So the correct way to think about this form of Ohm’s Law, is that resistance is proportional to the the voltage drop of the circuit between the points being measured. We can manipulate the voltage drop across that section by using a different resistor or combinations of resistors, or by adding or removing voltage sources.
Ohm’s Law Examples
Example 1
Let’s look at a simple circuit consisting of a battery and resistor:
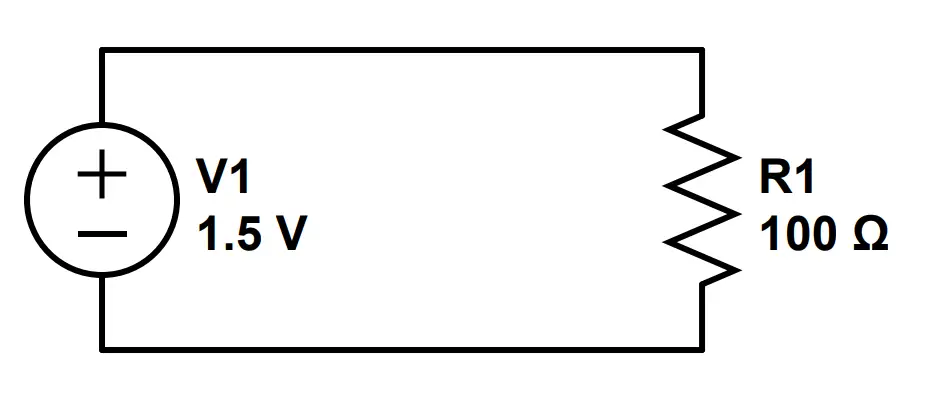
On the left we have a typical DC Voltage source; a 1.5 Volt Battery. We connect our battery terminals with a 100 Ohm resistor between, forming a circuit.
Reminder: It is always important to place at least one resistor in a circuit to prevent accidentally damaging the circuit and causing an unsafe condition.
Current in this circuit flows from the positive terminal of the battery clockwise through the resistor and into the negative terminal of the battery.
Let’s use Ohm’s Law to calculate the current:
I = \frac{V}{R} = \frac{1.5V}{100\Omega} = .015ASo, the current in this circuit is .015 amps.
Example 2
What happens if we replace the 100 Ohm resistor with a 5 Ohm resistor?
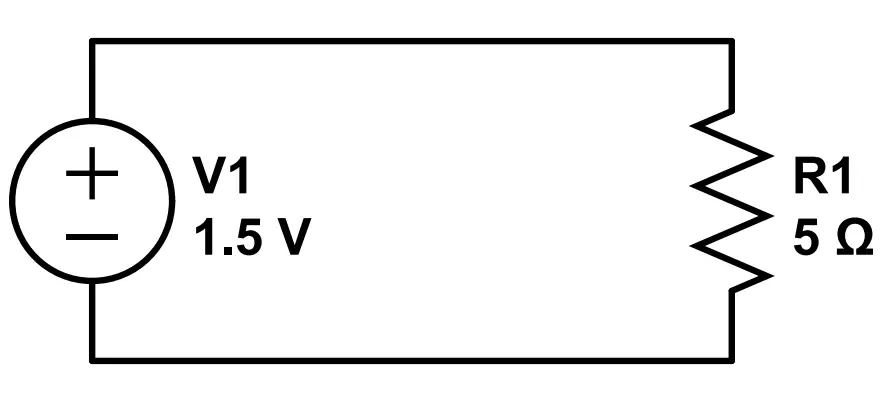
In this case:
I = \frac{V}{R} = \frac{1.5V}{5\Omega}=.3AWith a much lower resistance than in the first example, the current in the circuit is much higher. It is now .3 amps.
Example 3
We want to connect a new device to a 1.5 volt battery but it has a maximum current rating of .25 A. Determine the minimum value of resistor needed to protect the device.
Identify the value of the resistor needed:
R = \frac{V}{I} = \frac{1.5V}{.25A} = 6\OmegaTo protect our device, we will need to use a 6 Ohm resistor. In reality, we wouldn’t want the current in the circuit to approach the maximum current rating, so we would want to use a resistor with a higher value.
We will explore Ohm’s Law in much greater detail as we use it for examples and conceptual understanding in Module 3.
Before we tackle more complex circuits, let’s cover one more important concept in Lesson 7: Electric Power.