Capacitors

Why it’s important: Capacitors were one of the first electrical devices to be invented. The Leyden Jar is a type of capacitor used by Benjamin Franklin to prove that thunderstorms generate electricity. To this day, capacitors are one of the most important electronic components. Like resistors, they are found everywhere including both DC and AC circuits.
What is a Capacitor?
A capacitor is a device used to store electric charge. Like a battery, a capacitor can be used to store electrical energy and then release it when placed in a circuit.
There are a few key differences between batteries and capacitors. A battery stores potential energy in chemical form. A battery’s rate of discharge is limited by the chemical reactions in its’ electron producing and electron accepting cells.
A capacitor stores energy as an electric field, and can release this energy almost instantaneously.
| Device Type | Storage Amount | Rate of Discharge |
| Battery | Higher | Slow |
| Capacitor | Lower | Fast |
A capacitor is made of two electric conductors separated by an insulating material.
Capacitance
Let’s consider the example of a parallel-plate capacitor, which is made of two conducting plates separated by a distance, d.
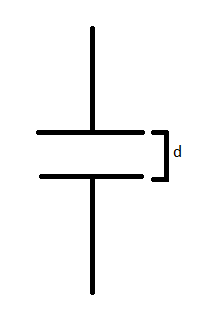
If we connect the two plates with a voltage source, charge will begin to accumulate on each plate. The schematic would look something like this:
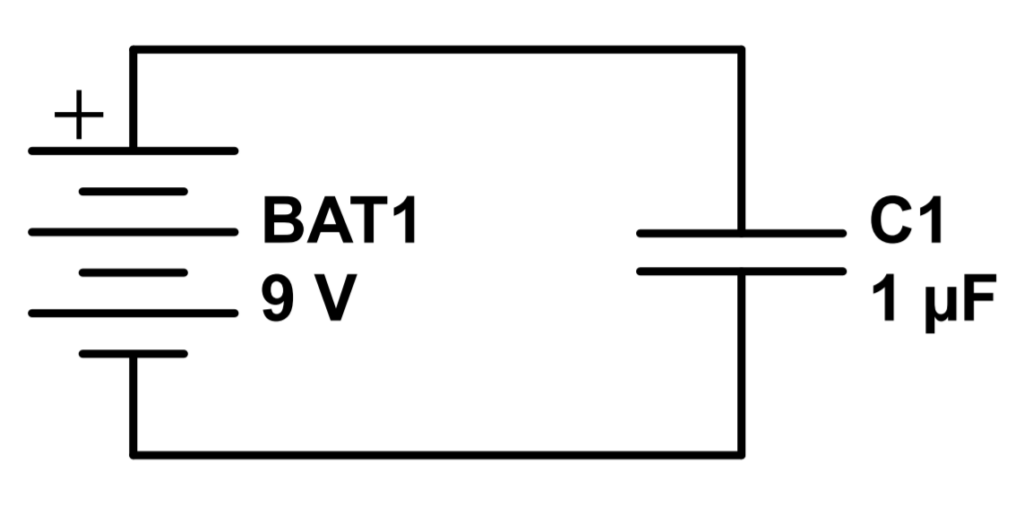
The top plate of the capacitor is connected to the positive terminal of the battery, so it will accumulate a positive charge. The bottom plate of the capacitor is connected to the negative terminal of the battery, so it will accumulate a negative charge.
As charge accumulates, the plates develop a voltage between them. If we leave the capacitor connected to the battery for long enough, the voltage between the capacitor plates will equal the voltage of the battery. The charge and the voltage are linearly proportional but using different materials, will result in a different amount of voltage for the same amount of charge. The ratio is called the capacitance:
C = \frac{Q}{V}Where Q is the charge (in Coulomb), V is the Voltage, and C is the capacitance.
Example 1:
a) How much charge will be stored in a 5uF capacitor connected to a 12 V battery?
Q = CV = (5*10^-6F)(12V)= 6*10^{-5} Cb) How much charge will be stored if we switch to a 24 V battery?
Q = CV = (5*10^{-6}F)(24V)= 1.2*10^{-4}CThe capacitor will hold twice as much charge if we double the voltage of the battery! We can do twice as much work!
c) Let’s keep the 24 V battery but swap the capacitor to a 50uF capacitor. How much charge will now be stored?
Q = CV = (50*10^{-6})(24V) = 1.2*10^{-3}CBy using a capacitor with 10x the capacitance, we can store 10x as much charge!
Keep in mind that all of these examples assume that the battery is connected long enough for the capacitor to charge completely.
SI Unit of Capacitance
The SI Unit of capacitance is the Farad, which is abbreviated as ‘F.
A Farad is defined as 1 Coulomb per Volt:
1F = \frac{1C}{1V}A Farad is a large unit of capacitance; most capacitors are defined using microfarads, or μF.
Capacitance and Energy
In the beginning of this article, we mentioned that capacitors store energy as well as charge.
We must use a bit of calculus in order to derive the relationship, but the final result is:
U = \frac{Q^2}{2C} = \frac{1}{2}QV = \frac{1}{2}CV^2Where U is the total potential energy stored in the capacitor, C is the capacitance, and V is the voltage.
We’ve also put together a comprehensive table of relative permittivity values for a wide variety of materials, which you can find here.