Kirchoff’s Current Law

Key Points:

  • Kirchoff’s Current Law (KCL) states that for any node (or junction) in a parallel circuit, the sum of currents entering the node (or junction) is equal to the sum of currents exiting the node (or junction).
  • KCL is a restatement of conservation of charge, specifically for nodes (or junctions) within a circuit.
  • KCL allows us to write an equation that sets the total sum of currents (positive for currents ‘in’, negative for currents ‘out’) equal to zero.

Kirchoff’s Current Law (KCL) is a simple observation that makes sense when you think about it. It’s really about the conservation of charge within a circuit.

In the most simple case, let’s pick any point in a circuit. Unless we somehow lose electrons, then the number of electrons going into that point will be the same as the number of electrons leaving that point. This is called conservation of charge. Charge (electrons) can’t just disappear.

Kirchoff’s Current Law is a restatement of conservation of charge, with the observation that it applies specifically to points where multiple current paths split or join. These are called nodes or junctions.

Definition of KCL:

Kirchoff’s Current Law states that the current going into a node or junction must be the same as the current leaving the node or junction.

Let’s start with the basics.

What’s a Node? What’s a junction?

A node is any point where two or more circuit elements meet. It also includes any interconnecting wires or conductors that are of equal potential at the actual junction point. Nodes are very similar to junctions but can have slight differences in definition.

Junctions are the point at which current branches off. Unlike nodes, they don’t usually include the connecting wires of equal potential.

You can think of junctions as the point of connection between multiple current paths, and nodes as the whole set of wires surrounding a junction. Nodes tend to encompass more of a circuit than junctions do.

Kirchoff’s Current Law (KCL) works equally well for junctions and nodes, but it is most commonly taught using nodes and is also known as the nodal rule. For the purposes of KCL, the difference between the two does not matter as long as you don’t switch between the two.

In other words, if you’re going to use KCL for a node, carry it all the way through and it will work. If you’re going to use KCL for a junction, do the same. Just don’t switch between using junctions or nodes halfway because it could lead to some confusion. If you have a few minutes, learn about nodes and junctions and you’ll quickly figure out why it can matter. We’ll point out junctions and nodes as we go over some examples, and you’ll quickly learn to spot them.

For a complete discussion on junctions and nodes, see our article here.

Kirchoff’s Current Law (also known as Kirchoff’s First Law)

The current going into a node is equal to the current exiting a node. Where else would the current go?

It sounds obvious, but the power of KCL is that it allows us to set up equations that can help us learn more about a circuit than Ohm’s Law can by itself.

We can pick any junction (or node), add the currents going into the node, subtract the currents leaving the node, and set the whole thing equal to zero. We’ll have a new equation that we can use with the values we already know, to calculate values that we didn’t know (or solve problems for class).

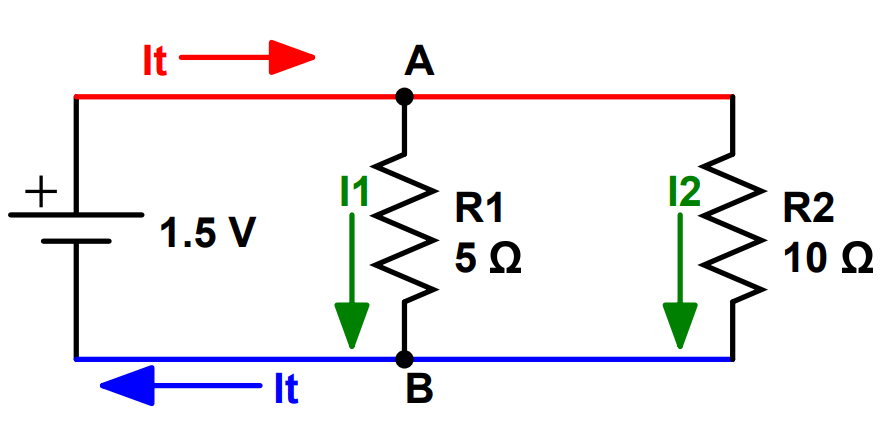
There are two nodes in this circuit, the red and blue conductors. There are also two junctions; one at point A and one at point B.

Let’s look at a simple example, that of two resistors in parallel. The first node is highlighted in red, and the second in blue. The nodes consist of the entire interconnecting sections of wiring between either side of the battery, R1, and R2. There are also two junctions, one at point A and another at point B.

KCL states that the current entering each node is equal to the current exiting each node.

For the first node, the current being supplied comes from the DC voltage source, a 1.5V battery. This current is labeled as IT because it is the total current that exits and enters the battery. The current enters the node and then splits at junction A, with some of the current exiting the node through R1 and some of the current exiting the node through R2. We’ve labeled these currents I1 and I2, respectively. These currents then recombine at junction B, which is inside the second node (identified in blue).

Let’s look at KCL for the first node. There is one current going into the node, IT. This current is positive because it’s adding to the current in the node. There are two currents exiting the node, I1 and I2. I1 and I2 are negative because they are subtracting from the current in the node. Let’s write out KCL for the first node:

I_T - I_1 -I_2 = 0 \\ I_T = I_1+I_2

Using Ohm’s Law, we can rewrite this as:

I_T = \frac{V}{R_1} + \frac{V}{R_2} = \frac{1.5V}{5\Omega} + \frac{1.5V}{10\Omega}=.3A+.6A=.9A

Steps to Using Kirchoff’s Current Law (KCL)

  1. Identify the nodes or junctions that you are trying to analyze. You can label them ‘Node A/B’, or ‘Junction A/B’ as appropriate.
  2. Try to guess as which node would be best to start with. It is probably the node that you already know the most about, and that feeds current to other nodes that you are trying to learn about.
  3. Write out KCL for the first node. Identify all the currents going into or out of the node or junction. Label them I1, I2, I3, I4, etc. Don’t worry if you don’t know which direction the currents are travelling. Don’t use the same label for two different current.
  4. Add up all of the currents and set the sum equal to zero. Solve for the current that you are trying to find. You can use Ohm’s Law to substitute voltage and resistance values in for unknown currents. If you find that a current is negative, that means that it is exiting a node.
  5. Repeat steps 3 and 4 for other nodes using the results you have already found.