What Are Dielectric Materials?

Dielectric materials are insulators that have a high degree of polarization when a voltage is applied across them. Another way of saying this is that they have high capacitance, or a high ability to store electric charge.
Because they can store a lot of electric charge, dielectric materials make excellent capacitors. Dielectrics are one of the most important types of material used in electronics. If you can understand how a dielectric becomes polarized, you will have a solid understanding of capacitors.
What are Dielectric Materials?
A dielectric material, or dielectric, is an insulator that can be polarized by an applied voltage.
Polarization means that when a voltage (potential difference) is placed across the material, the atoms and molecules in the material separate their charges a little bit in response to the voltage. One side of the material becomes a little more positively charged, and the other side becomes a bit more negatively charged.
This occurs because the voltage generates an electric field which then influences the atoms and molecules in the dielectric material. The image below shows how this happens. The ‘E’ indicates the direction of the electric field. An atom starts with its’ electrons in a spherical (represented as a circle) configuration.
When an electric field is applied, the electrons move, similarly to how a compass moves in response to the earth’s magnetic field.
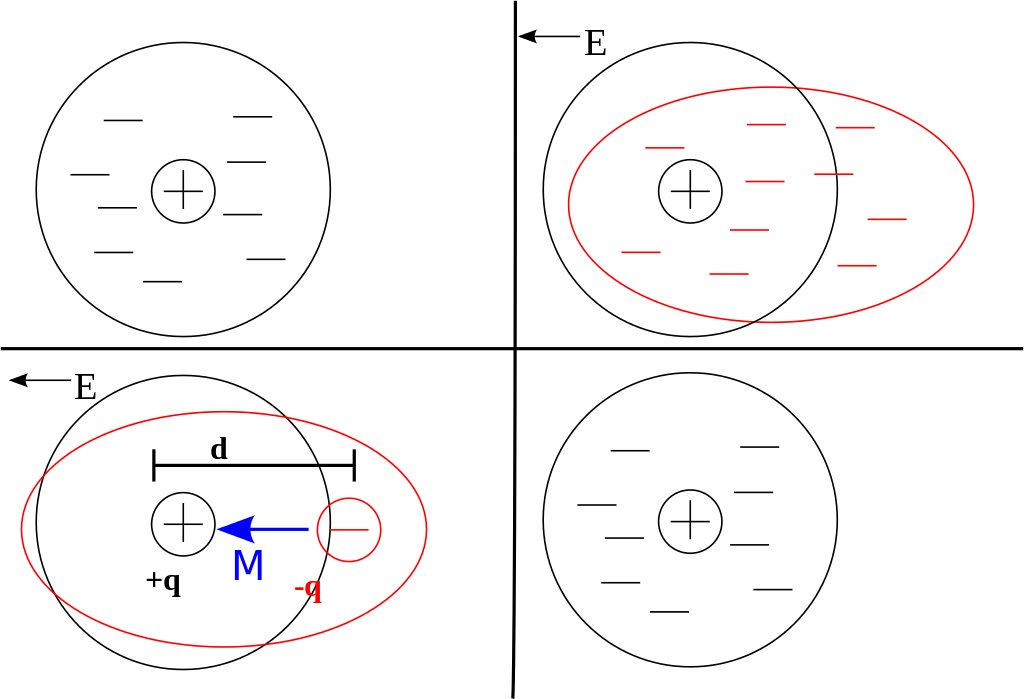
Some Technical Details (optional): The lower left frame gives us more detail. There is an overall separation of charge between the positive nucleus (+q) and the negative electrons (-q); this separation is represented by d. This gives rise to a dipole moment, M. The dipole moment M is a vector that represents the direction and magnitude of the charge separation.
Instead of conducting electricity, the atoms and molecules in a dielectric react to the electric field. The material becomes polarized; instead of being electrically neutral, one side accumulates a negative charge and the other accumulates a positive charge.
This happens both at the atomic and molecular levels. In other words, just as the atoms experience charge separation, the same thing happens with entire molecules. The molecules that make up the dielectric shift just a little bit, contributing to the total charge separation in the dielectric.
Since a dielectric is an insulator, the charge does not flow through the circuit but instead forms an electric field that stores electrical energy. A capacitor will store energy up to the maximum voltage applied, like the voltage of the battery it is connected to. Then, when you disconnect the battery, reverse the battery, or create a current path, the energy from the capacitor will discharge into the circuit.
Polarization in Dielectrics
The simplest way to think about polarization is that the atoms or molecules in the dielectric rearrange themselves in response to the applied voltage. In a dielectric without a voltage applied, the atoms in the material sit in their normal configuration, with their electrons centered around the nucleus.
When we apply a voltage, an electric field is generated across the dielectric material. It’s electrons move positions slightly because they are attracted to the positive side. They shift so that they are a little closer to the positive side.
The atoms on the side of the dielectric that is connected to the positive terminal, will shift a little so that their negative charges are closer to the positive side. The atoms on the side connected to the negative terminal will shift so that their positive charges are just a bit closer to the negatively charged plate. Like a spring being compressed, the atoms or molecules respond to the voltage. When the voltage is released and the dielectric is allowed to relax, the atoms and molecules spring back to their normal positions, pushing the charges that have accumulated on the plates back through the circuit.
Dielectrics vs. Insulators
The terms ‘dielectric material’ and ‘insulator’ are often used interchangeably, but this clouds the purpose of each.
An insulator is a material that is selected because of its’ overall resistance to current flow. Think of the insulation around a wire; the point is not to store charge in the insulator, but to protect you from getting shocked.
A dielectric is an insulator that is used inside a capacitor because of its’ high polarizability. The main purpose of the material in the capacitor isn’t just to prevent a short circuit through the capacitor, but also to store the maximum charge possible. A great insulator with low polarizability would still technically work in a capacitor, but we would need to make the capacitor a lot larger to get the same effect.
Another point: Even though dielectrics are insulators because they don’t allow current to flow, a perfect insulator is not dielectric. This is because using a dielectric in place of an insulator could cause electric charge to build up where we don’t want it. So the perfect insulator is actually a poor dielectric; whereas a perfect dielectric would be both infinitely polarizable while featuring infinite resistance.
Where Does Capacitance Come From?
It’s important to note that capacitance is an inherent property of a device. The amount of charge that can be stored per volt is not a result of the applied voltage, nor of the charge itself. Instead, it is the result of the type of dielectric material used, and the construction of the capacitor. This is why it’s so important to have a basic understanding of dielectric materials.
If we increase the size (area) of the two capacitor, the total capacitance will increase. If we increase the distance between the two plates, the total capacitance will decrease. This is expressed by the following formula:
C = \epsilon \frac{A}{d}Here, ε is the permittivity of the dielectric used. Permittivity is a constant used to describe how easily a dielectric polarizes. It is basically a constant that tells us how good a material is at storing electrical energy. The higher the permittivity of a material, the higher the capacitance will be. This means that more charge can be stored per volt.
Capacitance and Permittivity
Permittivity is actually measured in Farads per meter; how much capacitance the material has per meter.
Even a vacuum has permittivity, which is eloquently called the vacuum permittivity. The vacuum permittivity has its own symbol, and is an important quantity in its own right. The symbol for vacuum permittivity is ε0, and its value is very small:
\epsilon_0 = 8.854×10^{-12} \frac{F}{m}The permittivity of any material is expressed by comparing it to the vacuum permittivity. This ratio is called the relative permittivity, which is sometimes written as εr and sometimes written as κ:
relative\hspace{1mm}permittivity = \epsilon_r = \kappa = \frac{\epsilon}{\epsilon_0}The permittivity of materials is usually expressed as relative permittivity. Vacuum has a relative permittivity of 1 by definition, and air is just a bit higher. Remember that the higher the relative permittivity, the higher the capacitance. A material with a high relative permittivity can store a lot more charge per volt than air. Here’s a table with permittivity values for some common materials:
| Material | εr |
| Air | 1.00058986 |
| Alcohol | 16-31 |
| Body Tissue | 8 |
| Glass | 3.7-10 |
| Mineral Oil | 2.1 |
| Paper | 1.4 |
| Vacuum | 1 (By Definition) |
| Water | 80.2 |
| Wood | 2-6 |
We’ve also put together a comprehensive table of relative permittivity values for a wide variety of materials, which you can find here.