Boolean Algebra
Boolean algebra is a mathematical system that uses the binary values of true and false (1 and 0) to evaluate logical expressions. Boolean algebra allows us to perform incredibly complex mathematical operations using only two binary values.
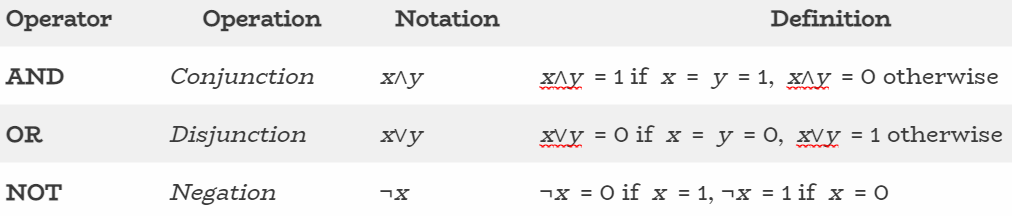
Boolean algebra is based on principles of logic and uses the binary values of 0 and 1 to represent and manipulate logical expressions.
It is used in computer science and electrical engineering to design and analyze digital circuits. In fact, virtually all digital circuits use the digits 0 and 1 because it allows the resulting circuit to use Boolean algebra to solve complex problems.
Ultimately, Boolean algebra allowed the creation of digital computers. This development caused an avalanche of new technologies, leading to the internet and much of our modern, technology based-culture and world.
Why Is Boolean Algebra is So Important?
Boolean algebra is an essential part of computer science and is used in many different ways in computers. One of the most important applications of boolean algebra in computers is in the design of digital circuits.
Digital circuits are circuits that use binary values (1s and 0s) to represent and manipulate data. These circuits are the building blocks of modern computers and are used in everything from simple devices like calculators to complex systems like servers and supercomputers.
Boolean logic is used in digital circuits to perform logical operations on the binary values that are input to the circuit. For example, a digital circuit might use boolean logic to determine whether a certain condition is true or false, such as whether a number is greater than or less than a certain value.
In addition to its use in digital circuits, boolean logic is also used in computer programming. Many programming languages, such as C, C++, and Java, have built-in boolean data types and operators that allow programmers to write code that performs logical operations on boolean values. This can be used to control the flow of a program, make decisions based on certain conditions, and perform other tasks that require logical reasoning.
Overall, boolean logic is a fundamental part of computer science and is used in many different ways in computers to perform logical operations and make decisions based on binary data.
History of Boolean Algebra
Boolean algebra was developed by the mathematician George Boole in the 19th century. Boole was interested in creating a mathematical system that could represent logical statements and operations.
His work, titled “An Investigation of the Laws of Thought,” was published in 1854 and outlined the principles of Boolean algebra. Boole’s work was later expanded upon by other mathematicians, such as Augustus De Morgan and John Venn, and is now a fundamental part of computer science and electrical engineering.
Over time, Boolean algebra gained increasing significance. Early digital computers were designed to make use of it using relays or vacuum tubes. Transistors eventually replaced vacuum tubes in computers, which became smaller and faster over time. Today, Boolean algebra can be found baked into the core of every cell phone, computer, laptop, and iOT device.
What are Binary Values?
Binary values are the two possible values used in Boolean algebra to represent true and false statements. The binary values are 0 and 1, where 0 represents false and 1 represents true. These values are used to represent and manipulate logical expressions in Boolean algebra. For example, the logical expression A AND B can be represented by the binary values 1 AND 0, which results in 0.
In digital circuits, a binary value of 0 is often represented by a low voltage or current, while a binary value of 1 is represented by a high voltage or current. Binary values are used to represent and manipulate logical expressions in Boolean algebra and are a fundamental part of computer science and electrical engineering.
Boolean Operations
Boolean operations are operations that take one or more boolean values (true or false) as input and produce a single boolean (true or false) output.
There are three basic boolean operations: conjunction (AND), disjunction (OR), and negation (NOT). These operations are performed on one or more input values, known as operands, to produce a single output value.
| Operator | Operation | Notation | Definition |
|---|---|---|---|
| AND | Conjunction | x∧y | x∧y = 1 if x = y = 1, x∧y = 0 otherwise |
| OR | Disjunction | x∨y | x∨y = 0 if x = y = 0, x∨y = 1 otherwise |
| NOT | Negation | ¬x | ¬x = 0 if x = 1, ¬x = 1 if x = 0 |
The three basic operations can be combined to perform more complex operations and, ultimately, run computer code.
AND Operation
The conjunction AND operation (denoted by the symbol ∧) produces a true output only if both of its operands are true. For example, the expression A ∧ B is true only if both A and B are true.
OR Operation
The disjunction OR operation (denoted by the symbol ∨) produces a true output if either of its operands are true. For example, the expression A ∨ B is true if either A or B (or both) are true.
NOT Operation
The negation NOT operation (denoted by the symbol ¬) negates the value of its operand. For example, the expression ¬A is true if A is false, and vice versa.
The Rules of Boolean Algebra
- The binary values of 0 and 1 can be used to represent true and false statements, respectively.
- The logical operations of AND, OR, and NOT can be applied to binary values to form logical expressions.
- The AND operation is represented by a dot (.) and results in a 1 only if both operands are 1.
- The OR operation is represented by a plus (+) and results in a 1 if either operand is 1.
- The NOT operation is represented by a bar (-) over the operand and negates the value of that operand, turning a true (1) into a false (0) and a false (0) into a true (1).
- The order of operations follows the same rules as standard algebra, with operations inside parentheses being performed first, followed by NOT, then AND, and finally OR.
- Any logical expression can be simplified by applying the rules of Boolean algebra and using the commutative, associative, and distributive properties.
Boolean algebra is a powerful tool for analyzing and designing digital circuits. It allows engineers to represent the logical relationships between different components in a circuit and to simplify complex expressions using the rules of Boolean algebra. It also allows for the creation of logical gates
Logic Gates
In digital electronics, a logic gate is a circuit element that performs a logical operation on one or more inputs and produces a single output. The most basic logic gates are the AND, OR, and NOT gates, which perform logical conjunction, disjunction, and negation, respectively. These basic gates can be combined to form more complex logical expressions and functions. Logic gates are the building blocks of digital circuits, and are used in a wide range of electronic devices, from simple switches to complex computers.