Capacitors in Series and Parallel

Why it’s important: Building on what we’ve learned about capacitors in series and in parallel, we can start analyzing more complex arrangements.
Review of Capacitance in Series and Parallel
Capacitance is the ratio of the total charge stored in the capacitor to the voltage drop across it:
C = \frac{Q}{V}We have previously learned about the equivalent capacitance of capacitors in parallel:
C_{Tparallel} = C_1 + C_2 + C_3 +...+C_NAs well as the relation for capacitors in series:
C_T = (\frac{1}{C_1}+\frac{1}{C_2}+...+\frac{1}{C_N})^{-1}Let’s combine these to analyze more complex circuits.
Example 1:
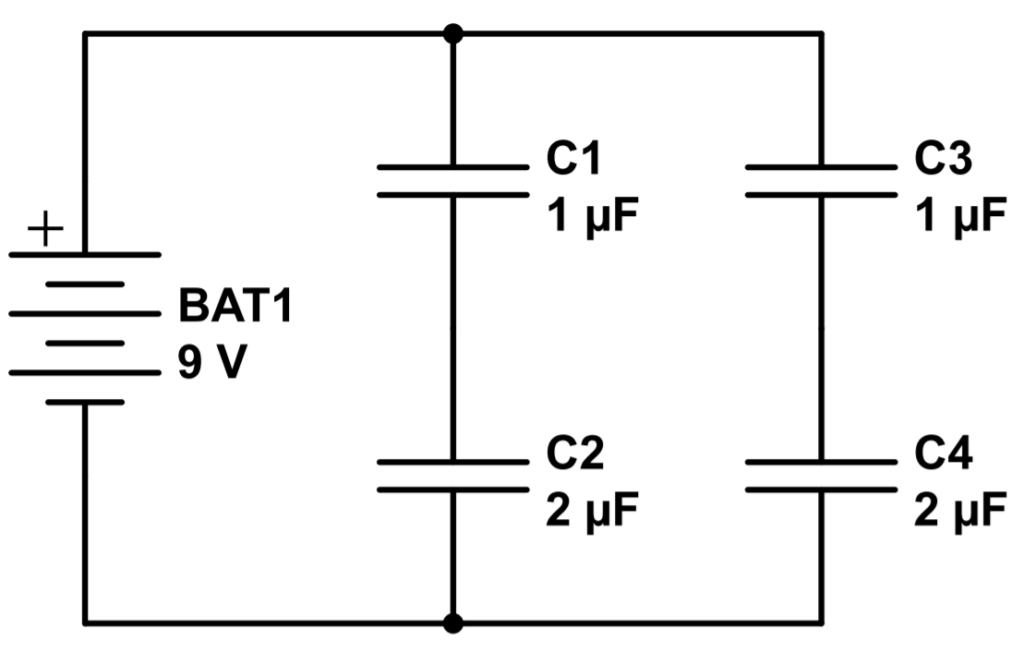
What happens when we see capacitors in combinations like in this example? The easiest way to divide this circuit is by first analyzing each parallel branch independently.
Q: What is the equivalent capacitance of this circuit?
Let’s start with the first path, consisting of C1 and C2. We’ll call the capacitance of this path CT1. In this case, the two capacitors are in series so we’ll use the relation for capacitors in series:
C_{T1} = (\frac{1}{C_1}+\frac{1}{C_2})^{-1}=(\frac{1}{1\mu F}+\frac{1}{2\mu F})^{-1} = \frac{2}{3}\mu FLet’s use the same procedure for the second branch:
C_{T2} = (\frac{1}{C_3}+\frac{1}{C_4})^{-1}=(\frac{1}{1\mu F}+\frac{1}{2\mu F})^{-1} = \frac{2}{3}\mu FThe two paths are identical, as they have the same capacitor arrangement.
The total capacitance for the circuit, then, treats each branch as a single capacitor with a value of 2/3 μF. We can now use the relation for capacitors in parallel to find the total equivalent capacitance of the circuit:
C_T = C_{T1} + C_{T2}= \frac{2}{3}\mu F+\frac{2}{3}\mu F=\frac{4}{3}\mu FExample 2:
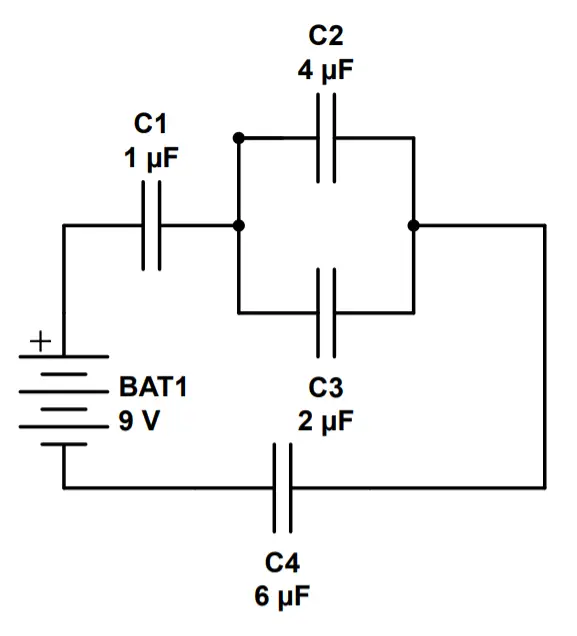
Q: What is the equivalent capacitance of this circuit?
In this case, we have two capacitors in series (C1 and C4), with C2 and C3 in parallel. We can ‘collapse’ C2 and C3 into an equivalent capacitor and then use the series circuit rule.
Let’s start by finding the equivalent capacitance of C2 and C3:which we will call Cp1
C_{p1} = C_2+C_3 = 4\mu F + 2\mu F = 6\mu FNow we can use the formula for capacitors in series to find the equivalent capacitance of the whole circuit:
C_T = (\frac{1}{C_1}+\frac{1}{C_{p1}}+\frac{1}{C_4})^{-1}=(\frac{1}{1\mu F}+\frac{1}{6\mu F}+\frac{1}{6\mu F})^{-1}=.75\mu F