Rust Bitwise Operators

In Rust, bitwise operators are used to interact with the binary representation of operands.

Bitwise operators can perform logical operations like AND, OR, NOT, and XOR as well as left and right shifting.

The following table summarizes the characteristics of bitwise operators in the Rust programming language:

Operator	Operation	Syntax	Description
&	AND	A & B	Bitwise AND
|	OR	A | B	Bitwise OR
!	NOT	!A	Bit inversion
^	XOR	A ^ B	Bitwise XOR
<<	Left Shift	A << B	Shift A left by B bits
>>	Right Shift	A >> B	Shift A right by B bits

What Are Bitwise Operators?

Bitwise operators are a category of operators that can be used to work with operands at the bit level. Instead of looking at the value of an operand, a bitwise operator looks at its’ bit representation.

Most of the bitwise operators perform a type of logic, and are thus similar to logical operators. These operators are essentially performing Boolean operations. However, bitwise operators operate at the bit level. This is in contrast with logical operators, which act on Boolean values themselves.

Bitwise AND

The bitwise AND operator acts like an AND gate between the bits of two operators. To see how this works, we need to look at the bit representation of each operator. Let’s say we have two integer operands, A and B. The operand A has a value of ‘5’, and B has a value of ‘9’. In terms of bit representation, a is equal to 0101 and b is equal to 1001. (The actual representation depends on the size of the integer, but this simplified example is good enough to show how bitwise operators work).

Operand A = 5 = 0101
Operand B = 9 = 1001

To recap, operand A is 5, which is represented in binary as ‘0101’. Operand B is equal to 9, which is ‘1001’.

Bitwise AND looks at each bit position and returns one only if both operands have a 1 in that position:

A & B = 0001

In this case, the bitwise AND operator outputs a value of 1 because only the right-most digit has a ‘one’1’ in both operands:

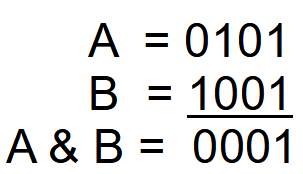
So A & B is equal to 0001, or just ‘1’. In practice, the actual bit values are abstracted (i.e. we don’t see the bit values in the code.)

Standard Output:

Bitwise AND: a & b: 1

Bitwise AND Truth Table

The following truth table summarizes the operation of Bitwise AND in Rust:

Operand A	Operand B	A & B
1	1	1
1	0	0
0	1	0
0	0	0

Bitwise OR

The bitwise OR operator acts like an OR gate between the bits of two operators. If you understand bitwise AND, you can easily apply the same concept to bitwise OR. Let’s take the same two operands A and B:

Operand A = 5 = 0101
Operand B = 9 = 1001

Bitwise OR looks at each bit position and returns one only if at least one operand has a bit in that position:

A | B = 1101 = 13

The bitwise OR operator outputs a value of ‘1101’, which is equal to 13.

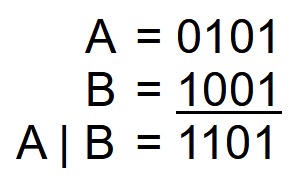
Again, the actual operation of the bits is abstracted from the code:

Standard Output: 

Bitwise OR: a | b: 13

Bitwise OR Truth Table

The following truth table summarizes the operation of Bitwise OR in Rust:

Operand A	Operand B	A | B
1	1	1
1	0	1
0	1	1
0	0	0

Bitwise NOT

The bitwise NOT operator inverts the value of each individual bit. Bits that have a value of ‘1’ are assigned the value ‘0’, and bits that a value of ‘0’ are assigned the value of ‘1’:

0 => 1
1 => 0

Bitwise NOT is a unary operator because it operates on a single operand. Let’s look at a trivial example of an operand, A, which is equal to 5:

A = 0101 (5)
!A = 1010 (10)

Bitwise NOT looks at each bit position and inverts the value of the bit. In the example above, we can see that !A is equal to 10.

However if we run the following code, we will find an unexpected result!

Standard Output:

Bitwise NOT: !a: -6

We get an output of -6, which is not what we were expecting. Why is this?

The variable ‘a’ has a default type of a signed 32 bit integer. This means that a value of 5 is not 0101 but rather:

a = 00000000000000000000000000000101 (5)

This means that NOT a (!a) is equal to the following:

!a = 11111111111111111111111111111010 (-6)

This number that looks rather large is actually equal to negative 6 (-6) in bitwise representation.

Bitwise NOT Truth Table

The following truth table summarizes the operation of Bitwise NOT in Rust:

Operand A	!A
1	0
0	1

Bitwise XOR

Bitwise XOR compares the bit representation of two operands and performs the XOR operation on them. XOR stands for exclusive or, a logical operation that is true if the two bits are different in value, i.e. one bit is zero (0) and the other is one (1).

Operand A = 5 = 0101
Operand B = 9 = 1001

Bitwise XOR looks at each bit position and returns one only if the two bit values at that position are different:

A ^ B = 1100

In this case, the bitwise XOR operator gives us the result 1100, which is equal to ’12’.

We can see this in the following example:

Standard Output:

Bitwise XOR: a ^ b: 12

Bitwise XOR Truth Table

The following truth table summarizes the operation of Bitwise XOR in Rust:

Operand A	Operand B	A ^ B
1	1	0
1	0	1
0	1	1
0	0	0

Left Shift

The bitwise left shift operator shifts the values to the left by adding zeroes to the right.

When the left shift operator is called, it will add the number of zeroes indicated by the second operand.

For example, a << b will take the bit representation of a and shift everything to the left by b number of bits. If b is two (2), then a’s bits will be shifted by adding two zeroes to the right.

A = 10 = 00001010
B = 2 = 00000010
A << B = A << 2 = 00101000

In this case, we added two zeroes to the right of A. A is now equal to 00101000, which is 40.

We can see this in action in the following code example:

Standard Output:

Left Shift: a << b: 40

Right Shift

The bitwise right shift operator shifts the values to the right by adding zeroes to the left.

When the right shift operator is called, it will add the number of zeroes indicated by the second operand.

For example, a >> b will take the bit representation of a and shift everything to the right by b number of bits. If b is two (2), then a’s bits will be shifted by adding two zeroes to the left.

A = 10 = 00001010
B = 2 = 00000010
A >> B = A >> 2 = 00000010

In this case, we added two zeroes to the left of A. To do so, we also removed two zeroes on the right. A is now equal to 00000010, which is 2.

We can see this in action in the following code example:

Standard Output:

Left Shift: a << b: 40